تصحيح الامتحان الوطني لمادة الرياضيات الدورة العادية 2008

التمرن األول لدنا الفلكة معرفة بالمعادلة التالة S x 2 y 2 z 2 2x 4z 2 0 S x إذن 2 2x y 2 z 2 4z 2 0 إذن فلكة مركزها 102 و شعاعها 3 لدنا O 000 A 0 11 B 1 10 إذن OA 0 11 OB 1 10 O إذن 111 هو مثلوث احداثات المتجهة O لتكن نقطة من المستوى AO منظمة على المستوى AO O بما أن المتجهة O 0 O O فإن متعامدتان أي O عن x y z 1 1 1 x y z 0 إذن 0 و هذه الكتابة األخرة عبارة عن معادلة دكارتة للمستوى AO لدنا 0 AO و لدنا كذلك فلكة مركزها 102 و شعاعها 3 إذن المستوى AO مماس للفلكة ف نقطة واحدة لدنا AO A 2 و لدنا أضا 2 z 2 2x 4z 2 0 0 أن نالحظ 2 1 2 1 2 2 0 4 1 2 0 إذن A من 1 و 2 نستنتج أن ه نقطة تماس AO و الفلكة التمرن الثان 2 6z 34 0 لنحل ف C المعادلة التالة 6 نالد 2 4 34 36 136 100 10i 2 1 و 2 إذن المعادلة تقبل حلن عقدن لدنا 4 2 fa و اإلزاحة معرفة بما ل لدنا M M إذن حسب التعرف المتجه لإلزاحة نكتب M fa عن و منه M fa z 4 2i z أي z 4 2i إذن نستنتج أن 4 2 fa fa و منه حسب الكتابة العقدة نستنتج أن A C لدنا aff A a 3 5i aff B b 3 5i aff C c 7 3i و بالتال و بالتال BA قائم الزاوة ف النقطة و A 2 B S x 1 عن 2 y 2 z 2 2 3 2 d OAB 1 0 2 1 2 1 2 1 2 3 3 3 z1 6 10i 2 3 5i و z2 6 10i 2 3 5i Tu P P M z M z b c a c 2i لدنا حسب ما سبق a c 2i aff A 4 2i 3 5i 4 2i نالد 7 3i aff C و بالتال اإلزاحة معرفة بما ل P P M z M z 4 2i إذن a c 3 5i 7 3i 3 5i 7 3i 4 8i 4 2i 4 8i 2i 4 2i 4 2i 4 16 16 40i 2i 2 4 2 40i 20 2i إذن b c a c 2i arg b c a c arg 2i 2 إذن b c a c 2 arg b c a c 2 2 عن b c 2 a c CA CB 2 2 A2 B عن AC B 90 و منه O O 1 1 1 1 1 1 1 0 i 0 1 1 0 j 0 1 1 1 k 1i 1 j 1k i j k 1 2 أ 2 2 ب 2 2 ج 1 O و O O 1 2 wwwbacdocma

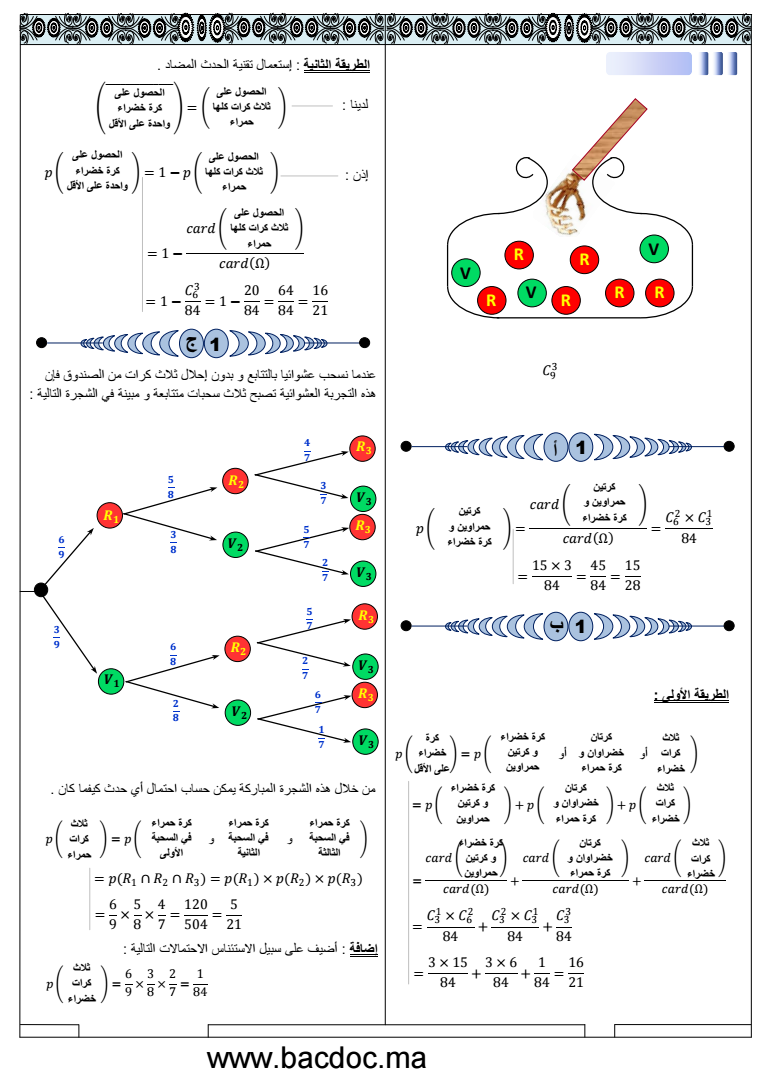
التمرن الثالث عندما نسحب عشوائا و ف آن واحد ثالث كرات من كس حتوي على 9 كرات فإن هذه التجربة العشوائة تحتمل نتجة ممكنة card C عن 9 3 84 بحث هو كون إمكانات هذه التجربة العشوائة لإلجابة على هذا السؤال أقترح طرقتن الطرقة األولى الطرقة الثانة إستعمال تقنة الحدث المضاد عندما نسحب عشوائا بالتتابع و بدون إحالل ثالث كرات من الصندوق فإن هذه التجربة العشوائة تصبح ثالث سحبات متتابعة و مبنة ف الشجرة التالة من خالل هذه الشجرة المباركة مكن حساب احتمال أي حدث كفما كان إضافة أضف على سبل االستئناس االحتماالت التالة V V V R R R R R R V2 R3 V3 3 8 5 8 4 7 5 7 2 7 R2 2 8 6 8 5 7 6 7 1 7 R1 V1 R2 R3 R3 R3 V3 V3 V2 3 7 2 7 V3 6 9 3 9 كرتن حمراون و كرة خضراء p card card C6 2 C3 1 84 15 3 84 45 84 15 28 كرتن حمراون و كرة خضراء ثالث كرات خضراء كرة خضراء و كرتن حمراون كرتان خضراوان و كرة حمراء p p p C3 1 C6 2 84 C3 2 C3 1 84 C3 3 84 3 15 84 3 6 84 1 84 16 21 كرة خضراء على األقل أو أو كرة خضراء و كرتن حمراون كرتان خضراوان و كرة حمراء ثالث كرات خضراء card card card card card card ثالث كرات خضراء كرة خضراء و كرتن حمراون كرتان خضراوان و كرة حمراء الحصول على كرة خضراء واحدة على األقل الحصول على ثالث كرات كلها حمراء لدنا إذن 1 C6 3 84 1 20 84 64 84 16 21 p 1 p الحصول على كرة خضراء واحدة على األقل الحصول على ثالث كرات كلها حمراء 1 card card الحصول على ثالث كرات كلها حمراء ثالث كرات حمراء كرة حمراء ف السحبة األولى كرة حمراء ف السحبة الثانة كرة حمراء ف السحبة الثالثة و و p R1 R2 R3 p R1 p R2 p R3 6 9 5 8 4 7 120 504 5 21 ثالث كرات خضراء p 6 9 3 8 2 7 1 84 1 أ 1 1 ب ج C9 3 wwwbacdocma

التمرن الرابع 1 112 C و هذا عن أننا نستطع حساب احتمال أي حدث وارد ف الشجرة بتتبع مساره فقط داخل الشجرة انتهت اإلضافة و الزادة من رأس العاقل لكن عنصرا من المجال 0 لدنا 2 ln إذن x x 2 ln x 1 2 x x2 x لكن عنصرا من المجال 0 2 عن 0 lt x 2 x 0 2 g عن x 0 إذن محور األراتب مقارب عمودي للمنحنى بجوار الصفر على المن و هذا عن أن الدالة تناقصة على المجال 0 2 لكن عنصرا من المجال 2 إذن 2 و منه 2 0 عن 2 x 0 عن أن الدالة تزادة على المجال 2 لكن عنصرا من المجال 0 هذا عن أن 0 2 أو 2 الحالة األولى لدنا 2 و بما أن تناقصة على 0 2 فإن 2 g 2 2 2 ln 2 06 gt 0 نالد و x 0 2 g x g 2 gt 0 إذن x 0 2 g x gt 0 عن الحالة الثانة لدنا 2 بما أن تزادة على 2 فإن 2 g 2 06 gt 0 نالد و x 2 g x g 2 gt 0 إذن x 2 g x gt 0 عن نالحظ أنه ف كلتا الحالتن لدنا 0 lt إذن من و نستنتج أن 0 g x gt 0 إذن لدنا إذن و لدنا كذلك إذن لدنا و هذه النهاات ت قبل فرعا شلجما ف اتجاه مكننا من أن نقول أن المستقم ذو المعادلة بجوار إذن 0 lt x x 2 x عن 2 x 2 x إذن lim x0 fx lim x ln x 2 x lim x ln x x ln x x lim x 2ln x x 2ln x x 4 lim x ln x x 2 4 lim t t x ln t t 2 4 0 2 0 lim x ln x 2 x lim x fx lim x x ln x 2 lim x x 1 ln x 2 x 1 0 lim x fx lim x fx x lim x x ln x 2 x lim x fx x 1 lim x f x x lim x x ln x 2 x lim x ln x 2 2 lim x f x x حصلنا لحد اآلن على النهاات التالة lim x fx lim x fx x 1 lim x f x x كرتن خضراون على األقل p 6 9 3 8 2 7 3 9 6 8 2 7 3 9 2 8 6 7 3 9 2 8 1 7 1 14 1 14 1 14 1 84 19 84 x 02 منه و 2 lt x 2 0 عن x 2 x 0 ln 0 2 0 2 0 lim x0 fx lim x0 x ln x 2 لدنا لدنا lim x 1 ln x 2 x 1 0 1 إذن 2 1 أ 1 أ 1 ب 2 ب 2 ج 2 II I II I I II II 1 2 1 112 C wwwbacdocma

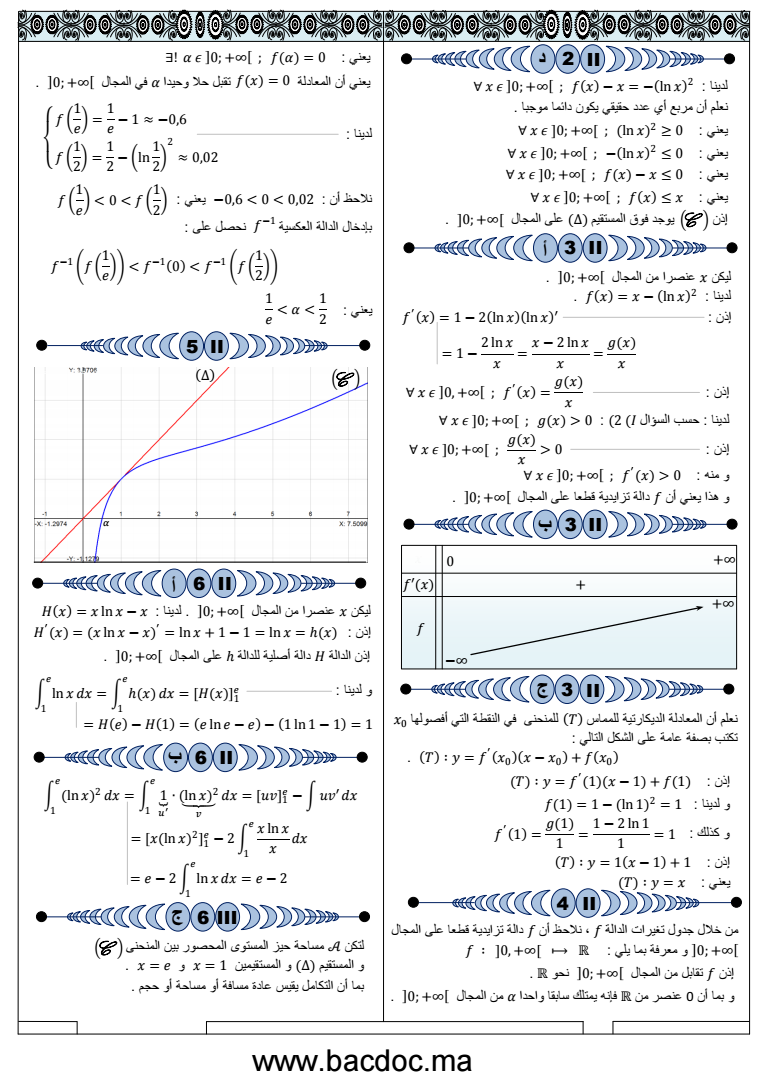
لدنا حسب السؤال 0 g x gt 0 2 x 0 f x x ln x نالد 2 نعلم أن مربع أي عدد حقق كون دائما موجبا x 0 ln x عن 2 0 x 0 ln x عن 2 0 x 0 f x x 0 عن عن 0 إذن وجد فوق المستقم على المجال 0 لكن عنصرا من المجال 0 2 لدنا ln إذن و منه 0 x gt 0 و هذا عن أن دالة تزادة قطعا على المجال 0 0 نعلم أن المعادلة الدكارتة للمماس للمنحنى ف النقطة الت أفصولها تكتب بصفة عامة على الشكل التال T y f x0 x x0 f x0 إذن 1 x 1 f 1 f 1 1 ln 1 نالد و 2 1 T y 1 x 1 1 إذن عن إذن تقابل من المجال 0 نحو R و بما أن 0 عنصر من R فإنه متلك سابقا واحدا من المجال 0 0 f 0 عن عن أن المعادلة تقبل حال وحدا ف المجال 0 لدنا بإدخال الدالة العكسة نحصل على لكن عنصرا من المجال 0 لدنا ln إذن x x ln x x ln x 1 1 ln x x إذن الدالة دالة أصلة للدالة على المجال 0 و لدنا لتكن مساحة حز المستوى المحصور بن المنحنى و المستقم و المستقمن 1 و بما أن التكامل قس عادة مسافة أو مساحة أو حجم ln x e 1 dx x e 1 dx Hx 1 e و كذلك 1 g1 1 1 2 ln 1 1 1 من خالل جدول تغرات الدالة نالحظ أن دالة تزادة قطعا على المجال 0 و معرفة بما ل 0 R f 1 e 1 e 1 06 f 1 2 1 2 ln 1 2 2 002 f 1 f 1 e lt f 1 0 lt f 1 f 1 2 f عن 06 lt 0 lt 002 أن نالحظ 1 e lt 0 lt f 1 2 عن 1 e lt lt 1 2 H e H 1 e ln e e 1 ln 1 1 1 x f fx 1 112 C إذن x 1 2 ln x ln x 1 2 ln x x x 2 ln x x gx x إذن 0 x gx x x 0 gx x gt 0 2 د 3 أ 5 3 ب 6 أ 3 ج 6 ب 6 ج 4 III II II II II II II II II 1 112 C f x 0 f 1 ln x 2 e 1 dx 1 u ln x 2 v e 1 dx uv 1 e uv dx x ln x 2 1 e 2 x ln x x e 1 dx e 2 ln x e 1 dx e 2 1 112 C wwwbacdocma

فإن لدنا حسب السؤال I 2 د 0 f x x 0 x 1 e f x x 0 إذن و منه 1 و كإضافة على هذا الجواب طلب منا ف بعض األحان حساب هذه المساحة 2 بالسنتمتر مربع c و من أجل ذلك نبحث عن وحدة المعلم c i j 3inu نفترض أن A e 2 lunit إذن 2 و ف حالة ما لم طلب منك ذلك فال داع لهذا كله أو كما قول المثل الابان الزادة من رأس األحمق Pn nN 1 un 2 ةالتال Pn نعتبر العبارة 1 u عن 1 2 2 نالد 0 2 0 إذن العبارة صححة nN 1 un 2 أن نفترض نعلم حسب السؤال I 3 أ أن الدالة تزادة على المجال 0 nN f1 fun f2 إذن 1 1 و لدنا f 2 2 ln 2 2 15 nN 1 f un 15 lt 2 إذن nN 1 f un عن 2 Pn nN 1 un1 2 منه و 1 إذن العبارة P صححة و بالتال حسب مبدأ الترجع N 1 un 2n لدنا حسب السؤال I 2 د 0 f x x 0 nN 1 un 2 نالد nN un 1 2 0 عن nN un 0 عن إذن نستطع تطبق النتجة من أجل u nN f un عن 0 u nN f un إذن u nN un عن 1 un u متتالة تناقصة و منه Nn nN 1 un 2 نالد u متتالة مصغورة بالعدد 1 إذن Nn و بما أنها تناقصة فه متقاربة أو بتعبر آخر و نهاتها l تحقق l l l ln l عن ln l عن 2 l 2 0 l 1 أي ln l 0 عن A f x x e 1 dx و بالتال e 1 dx x fx e 1 dx x x ln x 2 e 1 dx ln x 2 e 1 dx e 2 e 2 3 cm 2 9 e 2 cm2 A 1 112 C u مصغورة nN u تناقصة nN u متقاربة nN 3 1 2 III III III wwwbacdocma