La logique combinatoire

La logique combinatoire Rappels TS Rappels sur la logique combinatoire On utilisera les caractres 0 et 1 pour reprsenter les 2 tats binaires logique binaire Rappel En logique positive la plus employe le niveau logique haut quot1quot correspond la tension la plus haute du circuit Ex 5v le niveau logique bas quot0quot correspond la tension la plus basse du circuit Ex 0v Pour une variable active au niveau haut ltat logique quot1quot correspond laction activer valider Les variables dentre ou de sortie ou intermdiaires sont repres par des lettres ou initiales des fonctions ou signaux quils reprsentent souvent par rapport aux mots anglais Ex CEChip Enable autorisation du boitier Pour une variable active au niveau bas cest le quot0quot qui correspond laction Afin de pouvoir utiliser les 2 types de reprsentations sur un schma il est indispensable de distinguer laide dune barre au dessus des variables celles active ltat bas Ex si on trouve la variable CE1 et la variable CE2 alors il faudra un niveau 1 pour actionner le boitier 1 alors quil faudra un 0 pour actionner le boitier 2 Rappels des oprations logiques Ope ration ne gation non de la variable aa Opration ET AND de a et de b a b ab Opration OU OR de a avec b a b Opration NON ET NAND ab ab Opration NON OU NOR a b Opration OU exclusif EXOR a b ab ab Rappels sur les oprateurs et leur table de vrit S a b amp Sab S a b 1 1 1 0 0 Equation 0 et S a b Sab S a b 1 1 1 Equation 0 gt1 1 1 ou S a b amp Sab S a b 1 1 0 1 Equation 0 1 1 Nand S a b Sab S a b 1 1 0 0 0 0 Equation 0 gt1 Nor 1 LOGCOM3 Logique combinatoire Page 1

Rgles principales de lalgbre de Boole Ces rgles permettent de simplifier les quations logiques sans passer par la mthode des tableaux de KARNAUH aa 0 et a0 0 et a1 a a a 1 et a 1 1et a 0 a Distributivit de la fonction ET par rapport la fonction OU ab c ab ac Commutativit des fonctions ET et OU ab ba et a b b a Rappels sur les rgles de DE MORGAN Les rgles de De Morgan permettent de transformer les fonctions NAND et NOR en fonction ET ou en fonction OU et vis versa 1- fonction NAND ab a b 2- fonction NOR a b ab Rappels sur les tableaux de KARNAUGH Les tableaux de KARNAUGH permettent de simplifier des quations logiques sous forme graphique - Exemple de simplification directe Soit lquation logique de y une sortie en fonction des variables dentres a b c Il est possible de simplifier directement lquation logique laide des rgles de base en factorisant par ab le 1er et le 3eme terme et par bc le 2eme et le dernier terme En utilisant de nouveau les rgles de base on simplifie c c 1 et ab1 ab De mme a abc 1bc bc Dou lexpression simplifie de Y - Exemple de simplification en utilisant les tableaux de KARNAUGH Le tableau de Karnaugh reprsente ltat logique dune sortie en fonction des combinaisons des variables dentre On reprsente le codage des entres en binaire rflchi afin de ne changer quune seule variable dentre lorsquon se dplace dans le tableau dans le sens horizontal ou vertical dune case une autre case adjacente a bc 00 01 11 10 0 0 1 1 1 1 1 Tableau de KARNAUGH Equation Yabcabcabcabc 1 2 3 4 1 2 4 3 Codage binaire rflchi LOGCOM3 Logique combinatoire Page 2 S a b Sab S a b 1 1 0 0 1 Equation 0 1 1 Exor Y abc abc abc abc Y abc c a abc Y ab bc

Les simplifications laide du tableau se dduisent de regroupements graphique de cases Un regroupement correspond un ensemble de cases adjacentes le nombre de case doit tre une puissance de 2 ex 2 4 8 16 cases etc La forme des regroupements doit correspondre des rectangles ou des carrs Les regroupements les plus grands permettent dobtenir les quations les plus simples Lquation des regroupements est obtenue en regardant les variables qui ne change pas dtat Ex pour le regroupement N1 a change dtat donc nintervient pas dans lquation alors que b vaut toujours 0 et c vaut toujours 1 Lquation du 1er regroupement est donc bc Idem pour le 2eme a1 b1 mais c change dtat donc lquation est ab De lquation simplifie on en dduit le schma logique logigramme Lorsque les schmas sont complexes on indique souvent des variables intermdiaires de lquation ex soit X1ab et X2bc A Complment de cours sur les tableaux de KARNAUGH Rsolution de problme dalas Les tableaux de Karnaugh permettent dviter des problmes dalas tats indsirables des sorties lors du changement de certaines variables dentres Ces alas se produisent pendant des dures trs courtes et sont dus aux temps de propagation des portes logiques Attention les problmes dalas sont souvent trs difficile visualiser loscilloscope car leur dure quelques nS rend la visualisation parfois presque impossible Rem Il nest pas toujours indispensable de se proccuper des alas Lorsquune variation brve dune sortie ne peut pas entraner un dysfonctionnement ex transcodeur pour un systme daffichage Il nest pas gnant que laffichage soit perturb pendant un temps trs court Dtection dun alas Le tableau montre un problme dalas chaque fois que 2 regroupements sont adjacents et quil ny a pas dintersection Cest le cas dans lexemple vu prcdemment il y aura alas lorsque a1 c1 et b passant de 0 1 ou de 1 0 car on passe dun regroupement un autre alors quils sont adjacents LOGCOM3 Logique combinatoire Page 3 a bc 00 01 11 10 0 0 1 1 1 1 1 Equation 1 2 Ybcab regroupement 1 regroupement 2 a bc 00 01 11 10 0 0 1 1 1 1 1 alas a b c amp amp gt1 1 Y X1ab X2bc u1a u1b u2 u3

Explication du phnomne En observant les chronogrammes montrant les temps de propagation lors dun passage de 0 1 de b la sortie Y tait 1 avant grce au regroupement 1 et doit rester 1 aprs grce au regroupement 2 et vis versa lors du passage de 1 0 de b Le chronogramme de Y montre quil y a alas seulement lors dun passage de 1 0 de b La sortie Y a alors le temps de repasser 0 pendant le cours instant ou la porte U1a est dj 0 et ou la porte u1b nest pas encore 1 Solution au problme Il est possible de rsoudre les problmes dalas directement laide du tableau de Karnaugh Pour cela il suffit dajouter un ou des regroupements supplmentaires afin de ne plus avoir de regroupements adjacents Lquation de Y devient alors Y ab bc ac Le dernier terme ac supprime lalas car si a1 et c1 Y est obligatoirement 1 indpendamment de ltat ou des transitions de b Avantage des tableaux de Karnaugh dans le cas dtats indiffrents Dans certain cas ltude dun problme logique conduit un ou plusieurs tats impossibles Ex supposons que le systme logique ne permet pas davoir en mme temps b et c 1 Il nest donc pas ncessaire dimposer ltat de Y mais on choisira soit 0 soit 1 afin de simplifier les quations et donc dallger le schma On note les tats indiffrents par la lettre X Ici il est prfrable de prendre un regroupement de 4 cases et un de 2 cases Lquation de Y est alorsY c ab Le systme est alors beaucoup plus simple 2 portes suffisent 1 porte ET et une porte OU De plus il ny a plus de problme dalas LOGCOM3 Logique combinatoire Page 4 b t b t t t t ab bc Y alas porte ou sans temps tp tpHLporte inverseuse tpLHinverseur tpLHET u1a tpHLET u1a tpHLET u1b tpLHET u1b a bc 00 01 11 10 0 0 1 1 1 1 1 ajout dun regroupement a bc 00 01 11 10 0 0 1 1 1 1 X X a bc 00 01 11 10 0 0 1 1 1 1 X X

Regroupement de quot0quot avec les tableaux de Karnaugh Il est parfois plus facile de travailler avec le complment de la sortie Y lorsquil y a moins de 0 et ou lorsque les regroupements de 0 sont plus simples Dans le tableau ci-contre il faudrait 3 ou 4 regroupements 4 pour supprimer tout alas si on dsire crire lquation de Y Alors que lquation de Y ne ncessite que 2 regroupements SoitY bc abc On utilise alors les rgles de bases pour obtenir Y si besoin Y bc abc bc abc b cabcIl faut donc 1 porte OU une porte ET et une porte NAND 3 entres Inconvnient des tableaux de Karnaugh avec les fonctions OU exclusif Les tableaux de Karnaugh sont plus adapts dans le cas ou les solutions les plus courtes utilisent des portes de type ET OU et des inverseurs Dans le cas ou les quations se simplifieraient trs bien laide de portes NAND NOR EXOR ou EXNOR il est souvent difficile de le voir directement sur le tableau Il est donc indispensable de connatre parfaitement les rgles de base et celle de De Morgan Dans lexemple ci-contre les regroupements ne font quune case dou une quation complexeY abc abc abc abc Il ne reste plus que les rgles de lalgbre de Boole SoitY abc bc abc bc ab c ab c a b c Il suffit donc de 2 portes OU exclusif 2 entres nexiste pas en 3 entres Regroupements particuliers Il faut toujours penser que le bord gauche du tableau rejoint le bord droit comme si le tableau tait enroul sur un tube De mme le bord suprieur rejoint le bord infrieur Ainsi dans lexemple ci-contre lquation de Y correspond Y c B Autres normes de reprsentation des portes logiques inverseur a a a b ab porte ET a a a b ab porte NON ET a b ab porte OU tampon buffer NAND a b ab porte NON OU NOR a b a b porte EXNOR a b a b porte EXOR LOGCOM3 Logique combinatoire Page 5 a bc 00 01 11 10 1 1 1 1 Y 1 1 a bc 00 01 11 10 1 1 0 1 Y 1 0 1 a bc 00 01 11 10 1 1 1 0 Y 1 0 1 bord gauche bord droit

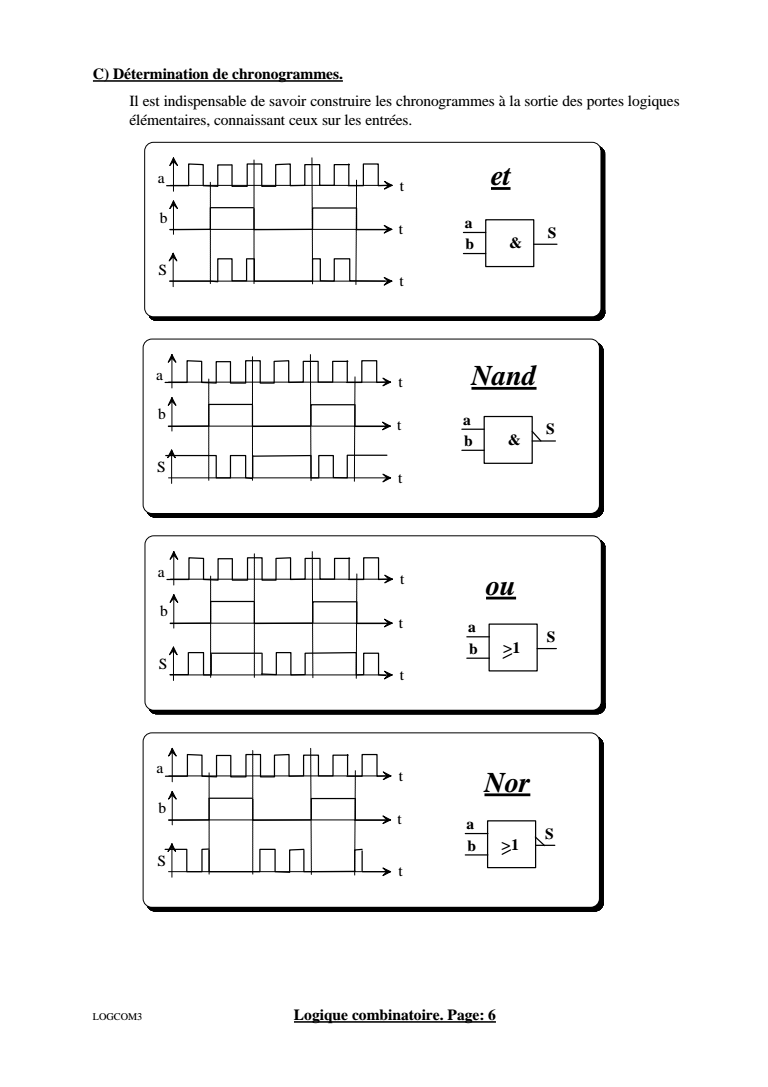
C Dtermination de chronogrammes Il est indispensable de savoir construire les chronogrammes la sortie des portes logiques lmentaires connaissant ceux sur les entres a t t t b S S a b amp et a t t t b S S a b amp Nand a t t t b S S a b gt1 ou a t t t b S S a b gt1 Nor LOGCOM3 Logique combinatoire Page 6

D Dtermination de fonction logique partir des chronogrammes Synthse Il est indispensable de savoir dterminer les quations logiques par construction dun tableau de Karnaugh partir des chronogrammes Il est alors possible de faire la synthse du systme logique et dobtenir le logigramme correspondant schma D Transformation en NAND ou en NOR Les quations obtenues partir du tableau de Karnaugh font souvent apparatre des fonctions OU ET et des inverseurs Il faut alors de nombreux botiers de circuits intgrs pour raliser la fonction logique sachant que les fonctions logiques sont regroupes par 2 3 4 ou 6 fonctions identiques dans un mme botier Ex 6 inverseurs dans un mme botier ou 4 portes 2 entres ou 3 portes 3 entres ou 2 portes 4 entres On transforme alors les quations pour ne conserver que des fonctions de mme type NAND ou NOR Rem On cherche plutt minimiser le nombre de botiers Ex pour la transformation en NAND il faut liminer toutes les fonctions OU par une S bdouble complmentation puis utilisation des rgles de De Morgan c ab bc ab Il faudra donc 4 portes NAND 1 par barre ce qui correspond 1 seul botier Rem La transformation en NOR est identique en suprimant toutes les fonctions ET laide des rgles de De Morgan a bc 00 01 11 10 0 0 1 1 1 1 1 1 2 4 Equation logique Sbcab regroupement 1 regroupement 2 a bc 00 01 11 10 0 0 1 1 1 1 1 a b c amp amp gt1 1 S X1ab X2bc u1a u1b u2 u3 1Reprsentation des chronogrammes dsirs 2 Elaboration du tableau de Karnaugh 3 Reprsentation des regroupements 5 Reprsentation du logigramme Attention Il faut dans la plupart des cas tudier les problmes dalas et rechercher les simplifications par utilisation de portes de type NAND ou NOR transformation de De Morgan A chaque changement dtat a b c ou S on rempli une case du tableau a t t S t b t c t1 Ex linstant t1 abcS0000 S S LOGCOM3 Logique combinatoire Page 7

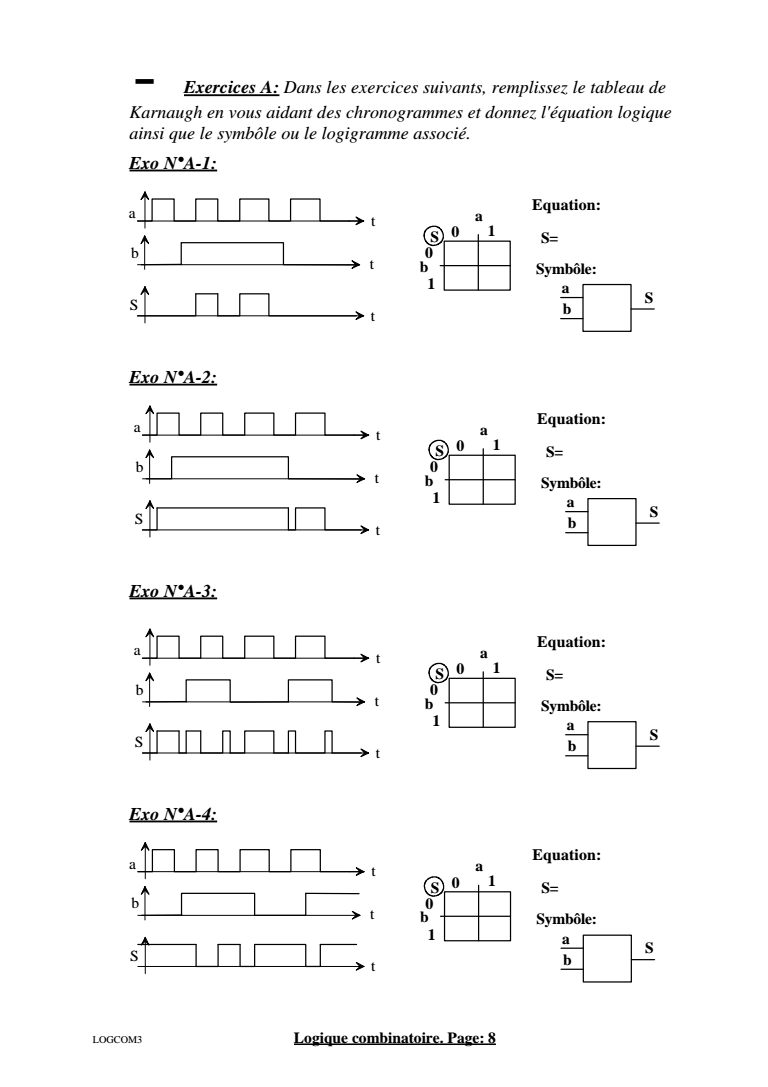
- Exercices A Dans les exercices suivants remplissez le tableau de Karnaugh en vous aidant des chronogrammes et donnez lquation logique ainsi que le symble ou le logigramme associ Exo NA-1 Exo NA-2 Exo NA-3 Exo NA-4 a t t t b S S a b Equation S a b 1 1 0 S Symble a t t t b S S a b Equation S a b 1 1 0 S Symble a t t t b S S a b Equation S a b 1 1 0 S Symble a t t t b S S a b Equation S a b 1 1 0 S Symble LOGCOM3 Logique combinatoire Page 8

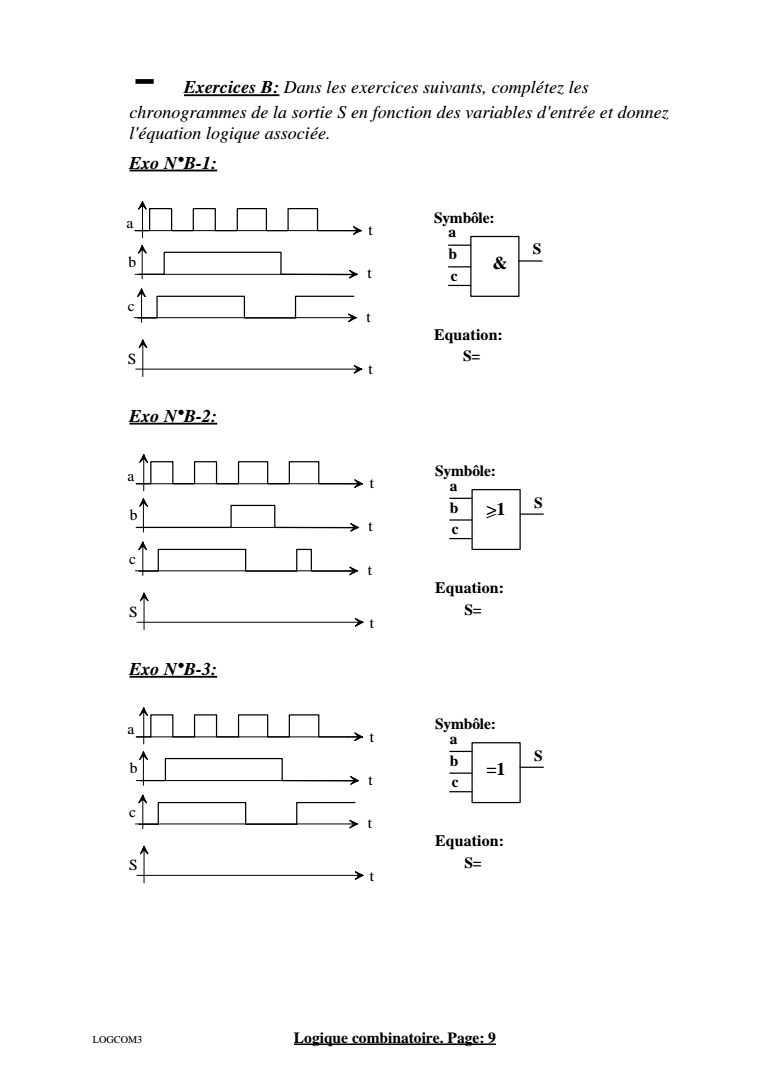
- Exercices B Dans les exercices suivants compltez les chronogrammes de la sortie S en fonction des variables dentre et donnez lquation logique associe Exo NB-1 Exo NB-2 Exo NB-3 a t t b S a b t S Equation S Symble t c c amp a t t b S a b t S Equation S Symble t c c gt1 a t t b S a b t S Equation S Symble t c c 1 LOGCOM3 Logique combinatoire Page 9

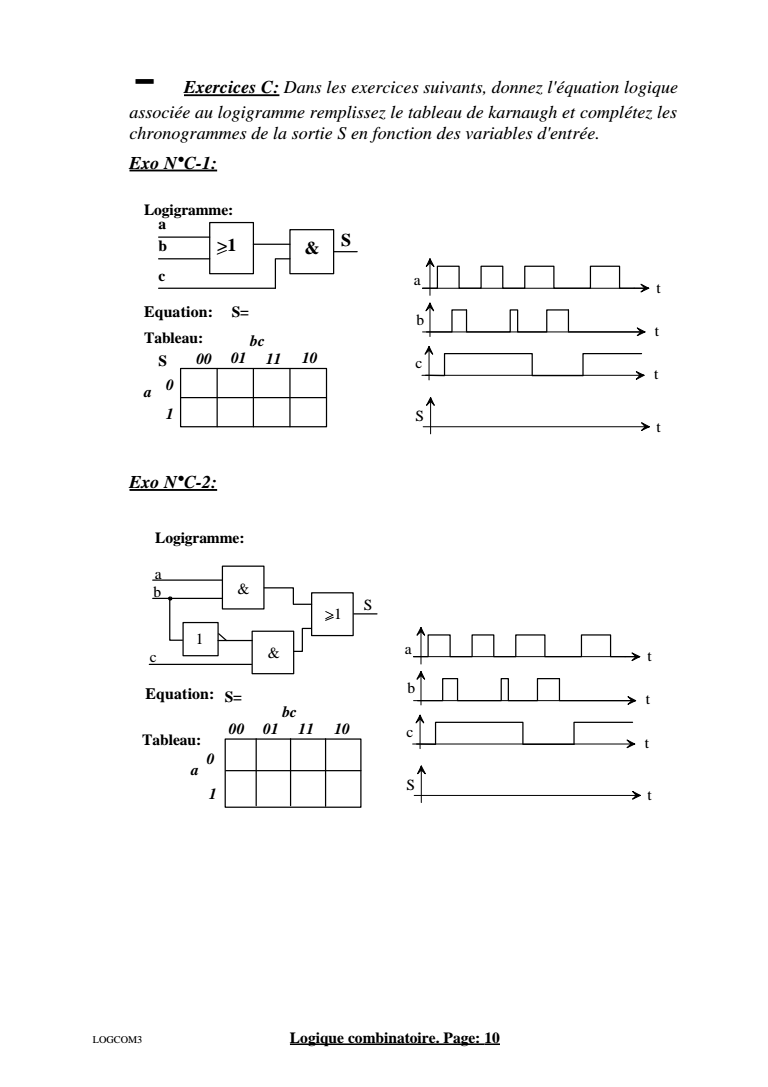
- Exercices C Dans les exercices suivants donnez lquation logique associe au logigramme remplissez le tableau de karnaugh et compltez les chronogrammes de la sortie S en fonction des variables dentre Exo NC-1 Exo NC-2 a t t b t S t c S a b Equation S Logigramme c gt1 amp a bc 00 01 11 10 1 Tableau S a t t b t S t c Equation S Logigramme a bc 00 01 11 10 1 a b c amp amp gt1 1 S Tableau LOGCOM3 Logique combinatoire Page 10